Decoherence and chaos
Real physical systems are never isolated and the coupling of the system to the environment leads to decoherence. This process can be understood as the loss of quantum information, initially present in the state of the system, when non-classical correlations (entanglement) establish between the system and the environment. On the other hand, when tracing over the environmental degrees of freedom, we expect that the entanglement between internal degrees of freedom of the system is reduced or even destroyed. Decoherence theory has a fundamental interest, since it provides explanations of the emergence of classicality in a world governed by the laws of quantum mechanics. Moreover, it is a threat to the actual implementation of any quantum computation and communication protocol. Indeed, decoherence invalidates the quantum superposition principle, which is at the heart of the potential power of any quantum algorithm. A deeper understanding of the decoherence phenomenon seems to be essential to develop quantum computation technologies.
Chaotic environments
The environment is usually described as a many-body quantum system. The best-known model is the Caldeira-Leggett model, in which the environment is a bosonic bath consisting of infinitely many harmonic oscillators at thermal equilibrium.
We have instead studied [1] the dynamics of the entanglement between two qubits coupled to a common chaotic environment, described by the quantum kicked rotator model, thus showing that the kicked rotator, which is a single-particle deterministic dynamical system, can reproduce the effects of a pure dephasing many-body bath. Indeed, in the semiclassical limit the interaction with the kicked rotator can be described as a random phase-kick, so that decoherence is induced in the two-qubit system. We have also shown that our model can efficiently simulate non-Markovian environments.


Non-Markovian effects in chaotic environments: oscillations of the entanglement decay  rate as a function of the classical chaos parameter (see [1]).

Quantum dephasing and internal chaos

It turns out that a moderately weak coupling to a disordered environment, which destroys the quantum phase correlations thus inducing decoherence, yields an exponential decay of the fidelity of quantum motion, with a rate which is determined by the system's Lyapunov exponent and independent of the perturbation (coupling) strength. In other words, quantum interference becomes irrelevant and the decay of fidelity is entirely determined by classical chaos. This result raises the interesting question whether the classical chaos, in the absence of any environmentstarts from a wide and incoherent mixed state (we remark in this connection that any classical device is capable of preparing only incoherent mixed states described by diagonal density matrices) then the initial incoherence persists due to the intrinsic classical chaos so that the quantum phases remain irrelevant. 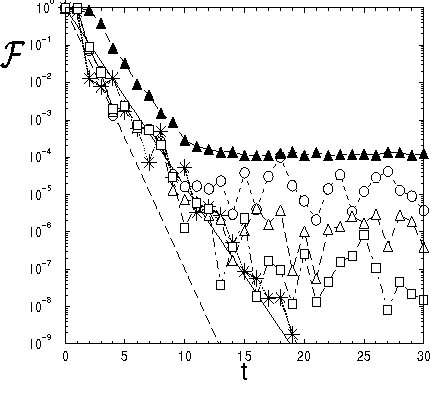In order to illustrate the quantum dephasing induced by classical chaos, we have introduced an extension of fidelity (which we named allegiance) for mixed states. The allegiance directly accounts for quantum interference and is measurable in a Ramsey interferometry experiment. We have shown that, in the semiclassical limit, the decay of this quantity is exactly expressed, due to the dephasing, in terms of an appropriate classical correlation function. Our results have been derived analytically for the case of a nonlinear driven oscillator and then numerically confirmed for the kicked rotor model. and only with a perfectly deterministic perturbation, can by itself produce incoherent mixing of the quantum phases (dephasing) strongly enough to fully suppress the quantum interference. The answer is, generally, negative. Indeed, even though the dynamics is chaotic, still there always exist a lot of very close trajectories whose actions differ only by terms of the order of Planck's constant. Interference of such trajectories remains strong. We have shown [2] that, nevertheless, if the system is classically chaotic and the evolution


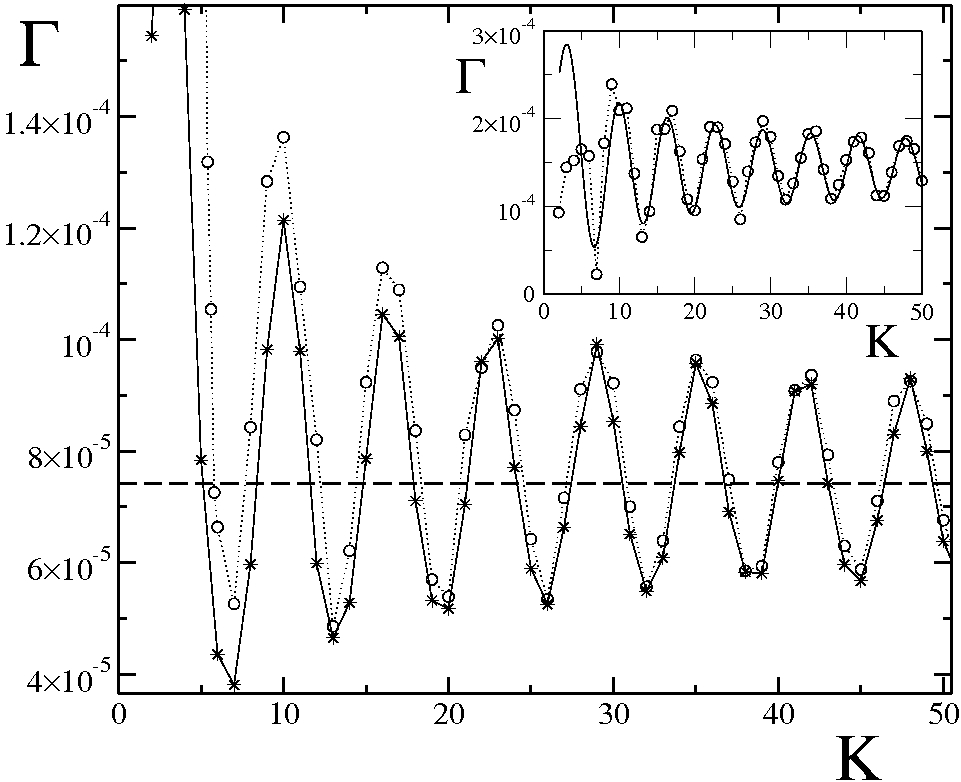
Decay of allegiance for the kicked rotor model (see [2])

Note that allegiance is  naturally measured in experiments performed on cold atoms in optical lattices and in atom optics billiard and proposed for superconducting nanocircuits [3]. This quantity is reconstructed after averaging the amplitudes over several experimental runs (or many atoms). Each run may differ from the previous one in the external noise realization and/or in the initial conditions drawn, for instance, from a thermal distribution. Note that the averaged (over noise) fidelity amplitude (that is, allegiance)can exhibit rather different behavior with respect to the averaged fidelity [3]



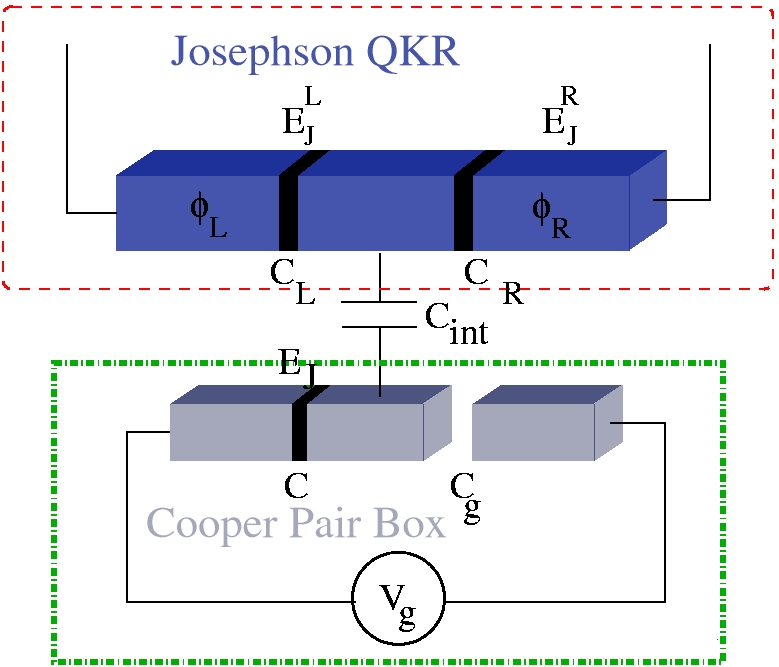
Schematic drawing of a superconducting device that might be used to measure allegiance: a Cooper pair shuttle (dashed red box) is capacitively coupled to a Cooper pair box (dot-dashed green box) (see [3]).


References
[1] D. Rossini, G. Benenti and G. Casati, Conservative chaotic map as a model of quantum many-body environment, Phys. Rev. E 74, 036209 (2006).
[2]  V.V. Sokolov, G. Benenti and G. Casati, Quantum dephasing and decay of classical correlation functions in chaotic systems, Phys. Rev. E 75, 026213 (2007).
[3]  S. Montangero, A. Romito, G. Benenti and R. Fazio, Chaotic dynamics in superconducting nanocircuits, Europhys. Lett. 71, 893 (2005).