In classical mechanics, complex systems are characterized by positive Lyapunov exponent i.e. by local exponential instability. They have positive algorithmic complexity and, in terms of the symbolic dynamical description, almost all orbits are random and unpredictable.
In spite of many efforts, the problem of characterizing the complexity of a quantum system is still open. Indeed the above notion of complexity cannot be transferred, sic et simpliciter, to quantum mechanics, where there is no notion of trajectories. Still, a comparison between classical and quantum dynamics can be made by studying the evolution in time of the classical and quantum phase space distributions, both ruled by linear equations.
We have proposed [1,2] the number of harmonics of the Wigner function as a suitable measure of the complexity of a quantum state. We recall that in classical mechanics the number of harmonics of the classical distribution function in phase space grows linearly for integrable systems and exponentially for chaotic systems, with the growth rate related to the rate of local exponential instability of classical motion. Thus the growth rate of the number of harmonics is a measure of classical complexity. Since the phase space approach can be equally used for both classical and quantum mechanics, the number of harmonics of the Wigner function appears as the correct quantity to measure the complexity of a quantum state.
We have shown [3] that this measure, which reduces to the well-known measure of complexity in classical systems and which is valid for both pure and mixed states in single-particle and many-body systems, takes into account the combined role of chaos and entanglement in the realm of quantum mechanics. The effectiveness of the measure has been illustrated in the example of the Ising chain in a homogeneous tilted magnetic field. We have provided numerical evidence that the multipartite entanglement generation leads to an exponential increase with time of the number of harmonics of the Wigner function until saturation in both integrable and chaotic regimes. The growth rate of the associated entropy can be used to detect quantum phase transitions. The proposed entropy measure can also distinguish between integrable and chaotic many-body dynamics by means of the size of long-term fluctuations which become smaller when quantum chaos sets in.
In this context, we have proposed [4] the Wigner separability entropy as a measure of complexity of a quantum state. This quantity measures the number of terms that effectively contribute to the Schmidt decomposition of the Wigner function with respect to a chosen phase space decomposition. We have proved that the Wigner separability entropy is equal to the operator space entanglement entropy, measuring entanglement in the space of operators, and, for pure states, to twice the entropy of entanglement. The quantum to classical correspondence between the Wigner separability entropy and the separability entropy of the classical phase space Liouville density is illustrated by means of numerical simulations of chaotic maps. In this way, the separability entropy emerges as an extremely broad complexity quantifier in both the classical and quantum realms.
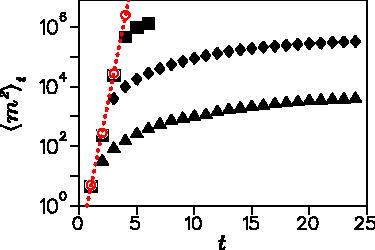
Growth of the number of harmonics in a chaotic system, both in quantum mechanics at different values of the effective Planck constant and in classical mechanics
References
[1] G. Benenti and G. Casati, How complex is quantum motion?, Phys. Rev. E 79, 025201(R) (2009).
[2] V.V. Sokolov, O.V. Zhirov, G. Benenti and G. Casati, Complexity of quantum states and reversibility of quantum motion, Phys. Rev. E 78, 046212 (2008).
[3] V. Balachandran, G. Benenti, G. Casati and J. Gong, Phase-space characterization of complexity in quantum many-body dynamics, Phis. Rev. E 82, 046216 (2010).
[4] G. Benenti, G.G. Carlo and T. Prosen, Wigner separability entropy and complexity of quantum dynamics, Phis. Rev. E 85, 051129 (2012).